:: 티칭백과 ::

< 목록

피타고라스 정리의 증명-가필드의 증명

피타고라스 정리의 증명-가필드의 증명

세 변의 길이가 \(a\), \(b\), \(c\)인 직각삼각형을 각각 \( a \)배, \( b \)배, \( c \)배 하여 닮은 삼각형 세 개를 만들어, 피타고라스 정리를 증명할 수 있다.

세 변의 길이가 \(a\), \(b\), \(c\)인 직각삼각형을 각각 \( a \)배, \( b \)배, \( c \)배 하여 닮은 삼각형 세 개를 만든다.

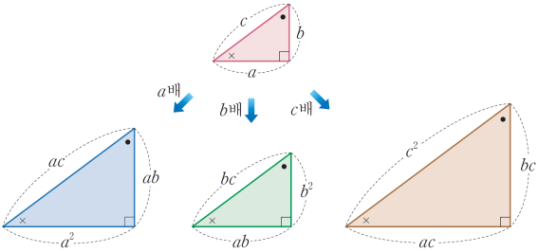
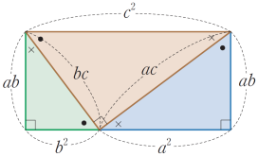
세 직각삼각형을 다음 그림과 같이 조합하면 직사각형이 되므로 \( a^2 +b^2 =c^2 \)이다.

출처 : 직접집필
관련교과서 : 금성 146쪽, 두산(강) 180쪽, 천재(이) 208쪽

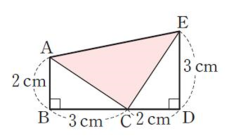오른쪽 그림에서 \(\angle{\textrm{B}}=\angle{\textrm{D}}=90^{\circ}\)이고 점 \(\textrm{B}\), \(\textrm{C}\), \(\textrm{D}\)가 한 직선 위에 있다. \(\overline{\textrm{AB}} = \overline{\textrm{CD}}=2 \textrm{cm}\), \(\overline{\textrm{BC}} = \overline{\textrm{DE}}=3 \textrm{cm}\)일 때, \(\triangle\textrm{ACE}\)의 넓이를 구하여라.: 정답확인하기; 정답 : \(\dfrac{13}{2} \textrm{cm}^2\) 해설 : \(\triangle\textrm{ABC}\equiv\triangle\textrm{CDE}\)이므로\(\qquad\)\(\angle{\textrm{ACE}}=90^{\circ}\) \(\triangle\textrm{ABC}\)에서\(\qquad\)\(\overline{\textrm{AC}} = \overline{\textrm{CE}}=\sqrt{ 2^2 + 3^2 }=\sqrt{13}(\textrm{cm}) \) 따라서 \(\qquad\)\(\triangle\textrm{ACE}=\dfrac{1}{2} \times \sqrt{13} \times \sqrt{13}=\dfrac{13}{2 }(\textrm{cm}^2) \)